括號對顏色高亮速度提升 10,000 倍

2021 年 9 月 29 日，作者 Henning Dieterichs，@hediet_dev

在 Visual Studio Code 中處理深度巢狀的括號時，很難弄清楚哪些括號匹配，哪些不匹配。

為了讓這一點更容易，在 2016 年，一位名叫 CoenraadS 的使用者開發了出色的 Bracket Pair Colorizer 擴充套件，用於為匹配的括號著色，並將其釋出到 VS Code Marketplace。這個擴充套件變得非常流行，現在是 Marketplace 上下載量排名前 10 的擴充套件之一，安裝量超過 600 萬。

為了解決效能和準確性問題，2018 年，CoenraadS 又推出了 Bracket Pair Colorizer 2，目前安裝量也超過 300 萬。

Bracket Pair Colorizer 擴充套件是 VS Code 可擴充套件性強大功能的一個很好的例子，它大量使用了 Decoration API 來為括號著色。

Two screenshots of the same code opened in VS Code. In the first screenshot, bracket pair colorization is disabled, in the second screenshot, it is enabled

我們很高興看到 VS Code Marketplace 提供了更多此類社群提供的擴充套件，所有這些擴充套件都以非常有創意的方式幫助識別匹配的括號對，包括：Rainbow Brackets、Subtle Match Brackets、Bracket Highlighter、Blockman 和 Bracket Lens。這些多樣化的擴充套件表明 VS Code 使用者確實渴望獲得更好的括號支援。

效能問題

不幸的是，Decoration API 的非增量特性以及缺少對 VS Code 令牌資訊的訪問，導致 Bracket Pair Colorizer 擴充套件在處理大檔案時速度緩慢：當在 TypeScript 專案的 checker.ts 檔案（包含超過 42k 行程式碼）開頭插入單個括號時，需要大約 10 秒才能更新所有括號對的顏色。在這 10 秒的處理過程中，擴充套件主機程序的 CPU 佔用率達到 100%，所有由擴充套件提供支援的功能（例如自動補全或診斷）都會停止工作。幸運的是，VS Code 的架構確保了 UI 保持響應，並且文件仍然可以儲存到磁碟。

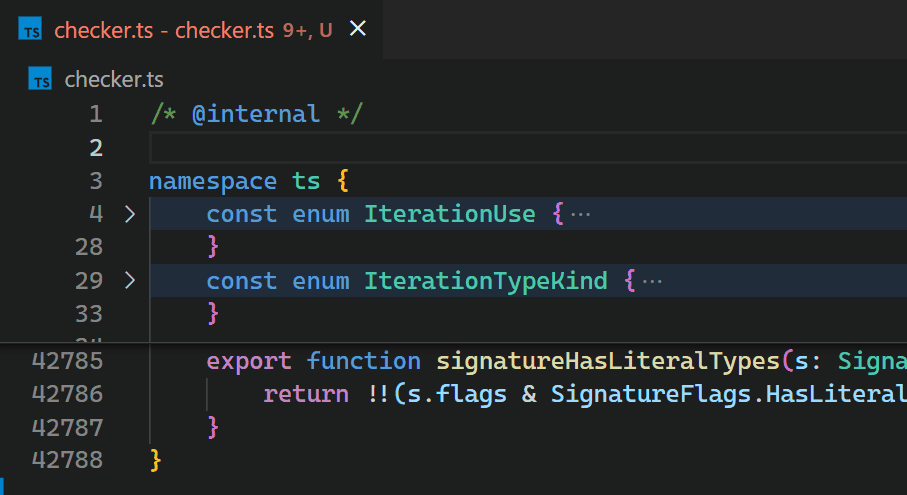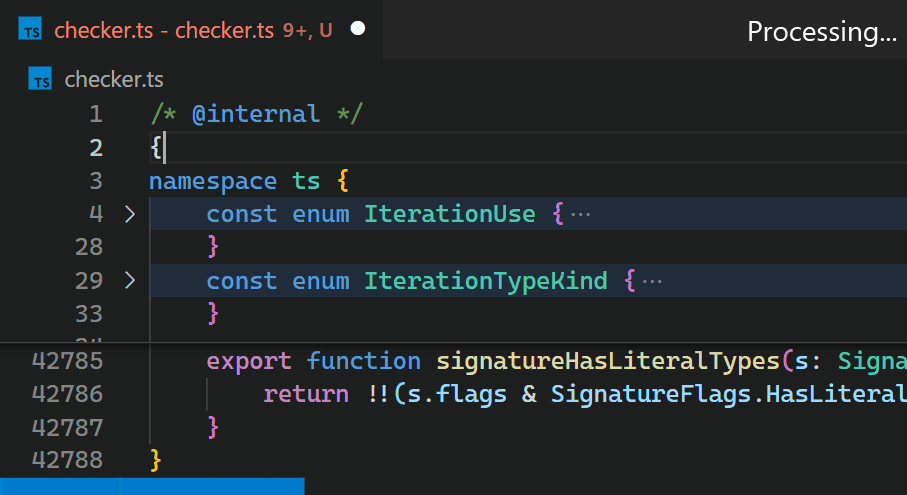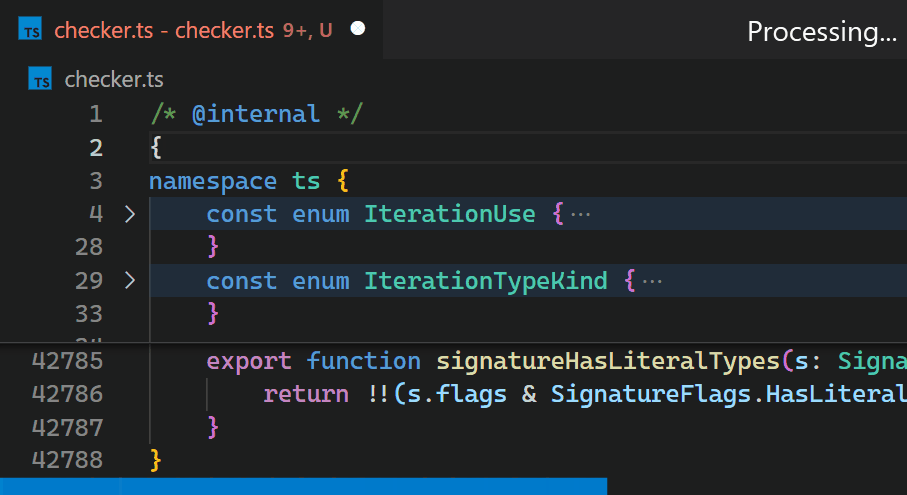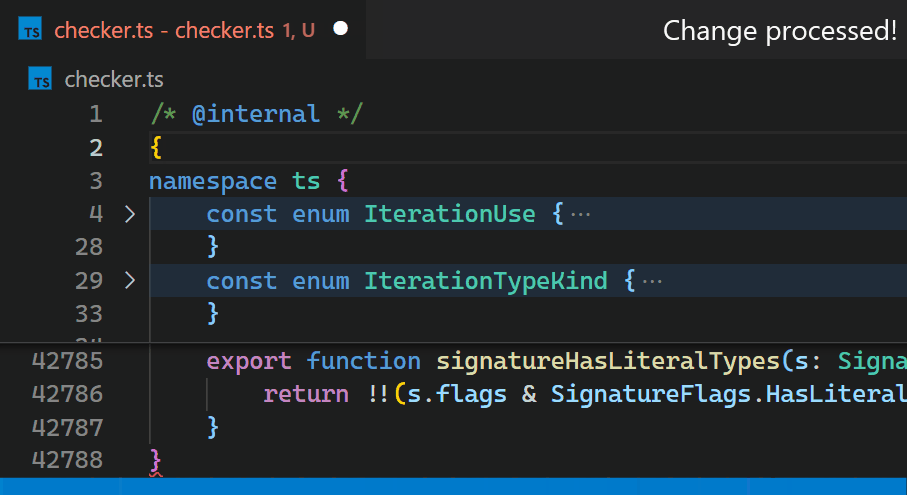
CoenraadS 意識到了這個效能問題，並投入了大量精力在擴充套件的第 2 版中提高了速度和準確性，透過重用 VS Code 的令牌和括號解析引擎。然而，VS Code 的 API 和擴充套件架構並非旨在在涉及數十萬個括號對時實現高效能的括號對顏色高亮。因此，即使在 Bracket Pair Colorizer 2 中，在檔案開頭插入 { 之後，顏色反映新的巢狀級別也需要一些時間

A video of VS Code showing that the extension needs more than 10 seconds to process the text change in checker.ts

雖然我們很樂意只改進擴充套件的效能（這肯定需要引入更高階的 API，針對高效能場景進行最佳化），但渲染器和擴充套件主機之間的非同步通訊嚴重限制了作為擴充套件實現時括號對顏色高亮的快慢。這個限制無法克服。特別是，不應在它們出現在視口中時立即非同步請求括號對顏色，因為這會在滾動大檔案時導致明顯的閃爍。有關此問題的討論可以在問題 #128465 中找到。

我們做了什麼

相反，在 1.60 更新中，我們在 VS Code 的核心中重新實現了該擴充套件，並將這個時間縮短到不到一毫秒——在這個特定的例子中，速度提高了 10,000 多倍。

可以透過新增設定 "editor.bracketPairColorization.enabled": true 來啟用該功能。

現在，即使對於包含數十萬個括號對的檔案，更新也幾乎察覺不到。請注意，在第 2 行輸入 { 後，第 42,788 行中的括號顏色會立即反映新的巢狀級別

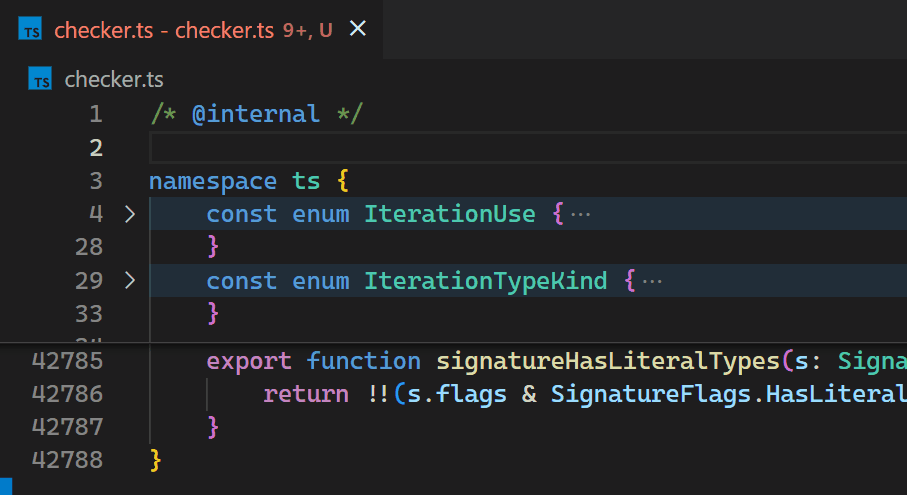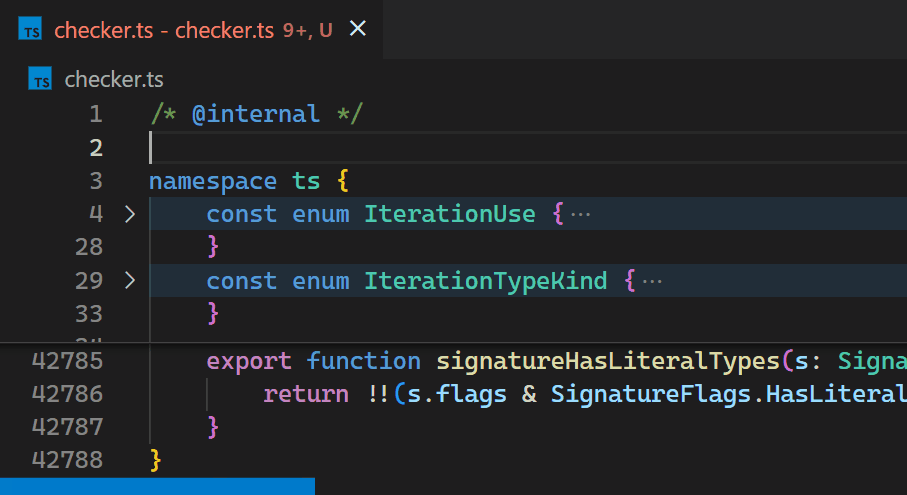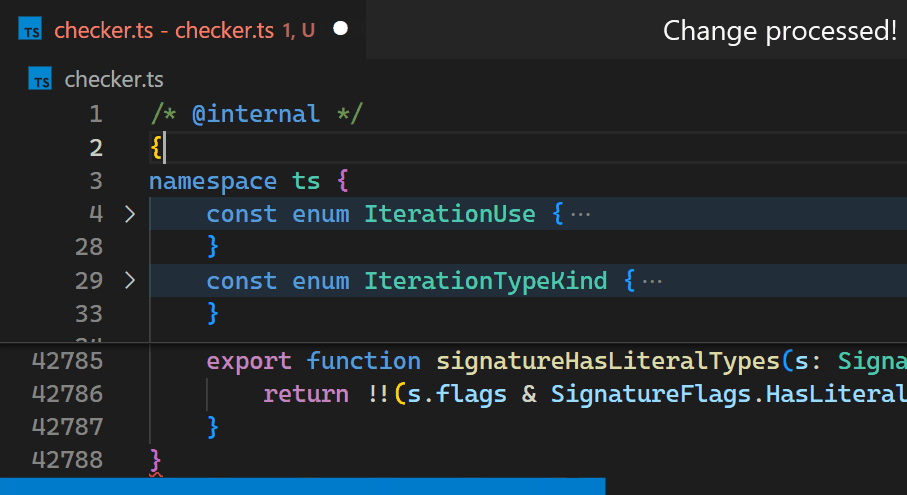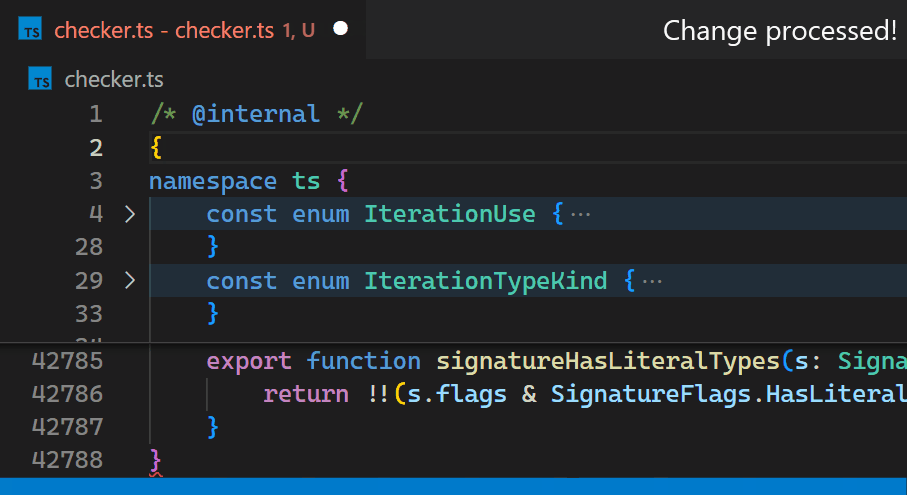
A video of VS Code showing that the native implementation needs less than a millisecond to process the text change in checker.ts

一旦我們決定將其移入核心，我們還藉此機會研究瞭如何使其儘可能快。誰不喜歡演算法挑戰呢？

在不受公共 API 設計限制的情況下，我們可以使用 (2,3)-樹、無遞迴樹遍歷、位運算、增量解析和其他技術來減少擴充套件在最壞情況下的更新時間複雜度（即當文件已經開啟時處理使用者輸入所需的時間），從 $\mathcal{O}(N + E)$ 到 $\mathcal{O}(\mathrm{log}^3 N + E)$ 其中 $N$ 是文件大小，而 $E$ 是編輯大小，假設括號對的巢狀級別上限為 $\mathcal{O}(\mathrm{log} N)$ .

此外，透過重用渲染器中的現有令牌及其增量令牌更新機制，我們獲得了另一個巨大的（但恆定的）速度提升。

Web 版 VS Code

除了效能更高之外，新的實現還支援 VS Code for the Web，您可以在 vscode.dev 和 github.dev 中看到它的實際應用。由於 Bracket Pair Colorizer 2 重用 VS Code 令牌引擎的方式，無法將該擴充套件遷移到我們所說的 web extension。

我們的新實現不僅適用於 VS Code for the Web，也直接適用於 Monaco Editor！

括號對顏色高亮的挑戰

括號對顏色高亮的全部意義在於快速確定視口中所有括號及其（絕對）巢狀級別。視口可以描述為文件中的一個範圍，以行號和列號表示，通常只佔整個文件的一小部分。

不幸的是，括號的巢狀級別取決於它前面的*所有*字元：將任何字元替換為開括號“{”通常會增加後面所有括號的巢狀級別。

因此，當最初為文件末尾的括號著色時，必須處理整個文件的每一個字元。

A diagram that indicates that changing a single character influences the nesting level of all subsequent brackets

bracket pair colorizer 擴充套件中的實現透過在插入或刪除單個括號時再次處理整個文件來解決這個挑戰（這對於小文件來說是非常合理的）。然後必須使用 VS Code Decoration API 刪除並重新應用顏色，該 API 將所有顏色裝飾傳送到渲染器。

如前所述，這對於包含數十萬個括號對（以及同樣多的顏色裝飾）的大文件來說是很慢的。因為擴充套件無法增量更新裝飾，必須一次性替換所有裝飾，所以 bracket pair colorizer 擴充套件也無法做得更好。儘管如此，渲染器以一種巧妙的方式組織所有這些裝飾（使用所謂的 interval tree），因此在收到（可能數十萬個）裝飾後，渲染速度總是很快的。

我們的目標是不必在每次按鍵時重新處理整個文件。相反，處理單個文字編輯所需的時間應該只隨文件長度呈（多重）對數增長。

然而，我們仍然希望能夠以（多重）對數時間查詢視口中的所有括號及其巢狀級別，就像使用 VS Code 的 decoration API（它使用前面提到的 interval tree）一樣。

演算法複雜度

請隨意跳過有關演算法複雜度的部分。

在下文中， $N$ 指的是文件的長度。更正式地說，我們的目標是查詢給定大小範圍內的所有括號時，時間複雜度至多為 $\mathcal{O}(\mathrm{log}^k N + R)$ 大小為 $R$ 的範圍，以及一個合理小的 $k$ （我們目標是 $k = 2$ ）。在渲染視口時查詢括號，因此查詢速度必須非常快。

然而，我們允許文件首次開啟時的初始化時間複雜度為 $\mathcal{O}(N)$ （這是不可避免的，因為最初為括號著色時必須處理所有字元），以及更新時間複雜度為 $\mathcal{O}(\mathrm{log}^j N + E)$ 當 $E$ 個字元被修改或插入時，對於一個合理小的 $j$ （我們目標是 $j = 3$ ）。我們還假設括號對的巢狀級別不會太深，至多為 $\mathcal{O}(\mathrm{log} N)$ 並且沒有開括號對應的閉括號數量可以忽略不計——違反這些假設的文件是不典型的，我們正在尋找的演算法不需要對它們保持快速。

語言語義使括號對顏色高亮變得困難

真正使括號對顏色高亮變得困難的是根據文件語言檢測實際的括號。特別是，我們不希望檢測註釋或字串中的開括號或閉括號，如下面的 C 示例所示

{ /* } */ char str[] = "}"; }

只有第三個出現的“}”才關閉括號對。

對於令牌語言不規則的語言（例如帶有 JSX 的 TypeScript）來說，這變得更加困難

Screenshot of TypeScript code, showing a function that contains a template literal with nested expressions. The template literal also contains a closing bracket at position 2. The function starts with the bracket at 1 and ends with the bracket at 3.

[1] 處的括號是否與 [2] 處或 [3] 處的括號匹配？這取決於模板文字表達式的長度，只有具有無限狀態（即非規則分詞器）的分詞器才能正確確定。

令牌來救援

幸運的是，語法高亮必須解決一個類似的問題：在前面的程式碼片段中，[2] 處的括號應該渲染為字串還是純文字？

事實證明，忽略語法高亮識別的註釋和字串中的括號對於大多數括號對來說效果足夠好。< ... > 是我們迄今為止發現的唯一有問題的一對，因為這些括號通常既用於比較，也用作泛型型別的對，同時具有相同的令牌型別。

VS Code 已經有一個高效的同步機制來維護用於語法高亮的令牌資訊，我們可以重用它來識別開括號和閉括號。

這是 Bracket Pair Colorization 擴充套件面臨的另一個挑戰，它對效能產生負面影響：它無法訪問這些令牌，必須自己重新計算它們。我們考慮了很久如何有效地、可靠地將令牌資訊暴露給擴充套件，但得出的結論是，如果不將大量實現細節洩露到擴充套件 API 中，我們就無法做到這一點。因為擴充套件仍然必須為文件中的每個括號傳送一個顏色裝飾列表，所以僅憑這樣的 API 甚至無法解決效能問題。

作為旁註，當在文件開頭應用編輯（例如為 C-like 語言插入 /*）更改所有後續令牌時，VS Code 不會一次性重新分詞長文件，而是隨著時間分塊進行。這確保了 UI 不會凍結，即使分詞是在渲染器中同步發生的。

基本演算法

核心思想是使用遞迴下降解析器來構建抽象語法樹 (AST)，描述所有括號對的結構。當找到一個括號時，檢查令牌資訊，如果它在註釋或字串中，則跳過該括號。分詞器允許解析器檢視和讀取此類括號或文字令牌。

現在的技巧是隻儲存每個節點的長度（並且為所有非括號的內容提供文字節點以填補空白），而不是儲存絕對開始/結束位置。僅有長度可用，仍然可以有效地在 AST 中定位給定位置的括號節點。

下圖顯示了一個帶有長度註釋的示例 AST

Abstract Syntax Tree of Bracket Pairs With Relative Lengths

將其與使用絕對開始/結束位置的經典 AST 表示進行比較

Abstract Syntax Tree of Bracket Pairs With Absolute Start/End Positions

兩個 AST 描述了相同的文件，但在遍歷第一個 AST 時，必須即時計算絕對位置（這很容易做到），而在第二個 AST 中它們已經預先計算好了。

然而，當在第一個樹中插入單個字元時，只需更新節點本身的長度及其所有父節點的長度——所有其他長度保持不變。

當像第二個樹中那樣儲存絕對位置時，文件中後面*每個*節點的位置都必須遞增。

此外，透過不儲存絕對偏移量，可以共享具有相同長度的葉節點以避免分配。

這是帶有長度註釋的 AST 在 TypeScript 中的定義方式

type Length = ...;

type AST = BracketAST | BracketPairAST | ListAST | TextAST;

/** Describes a single bracket, such as `{`, `}` or `begin` */
class BracketAST {
    constructor(public length: Length) {}
}

/** Describes a matching bracket pair and the node in between, e.g. `{...}` */
class BracketPairAST {
    constructor(
        public openingBracket: BracketAST;
        public child: BracketPairAST | ListAST | TextAST;
        public closingBracket: BracketAST;
    ) {}

    length = openingBracket.length + child.length + closingBracket.length;
}

/** Describes a list of bracket pairs or text nodes, e.g. `()...()` */
class ListAST {
    constructor(
        public items: Array<BracketPairAST | TextAST>
    ) {}

    length = items.sum(item => item.length);
}

/** Describes text that has no brackets in it. */
class TextAST {
    constructor(public length: Length) {}
}

查詢這樣的 AST 以列出視口中的所有括號及其巢狀級別相對簡單：執行深度優先遍歷，即時計算當前節點的絕對位置（透過加上前面節點的長度），並跳過完全在請求範圍之前或之後的節點的子節點。

這個基本演算法已經起作用了，但還有一些懸而未決的問題

我們如何確保查詢給定範圍內的所有括號具有所需的對數效能？
輸入時，我們如何避免從頭開始構建新的 AST？
我們如何處理令牌塊更新？當開啟大文件時，令牌最初不可用，而是分塊傳入。

確保查詢時間是對數的

當查詢給定範圍內的括號時，真正長的列表會破壞效能：我們無法對它們的子節點進行快速二分查詢以跳過所有不相關的非相交節點，因為我們需要對每個節點的長度求和才能即時計算絕對位置。在最壞的情況下，我們需要遍歷所有節點。

在下面的示例中，我們必須檢視 13 個節點（藍色）才能找到位置 24 處的括號

Long list in Abstract Syntax Tree

雖然我們可以計算並快取長度總和以啟用二分查詢，但這與儲存絕對位置有相同的問題：每次單個節點增長或縮小時，我們都需要重新計算所有這些值，這對於非常長的列表來說成本很高。

相反，我們允許列表將其他列表作為子節點

class ListAST {
  constructor(public items: Array<ListAST | BracketPairAST | TextAST>) {}

  length = items.sum(item => item.length);
}

這如何改善情況？

如果我們能確保每個列表只有有限數量的子節點並類似於對數高度的平衡樹，事實證明這足以獲得查詢括號所需的對數效能。

保持列表樹平衡

我們使用 (2,3)-樹來強制這些列表平衡：每個列表必須至少有 2 個且至多 3 個子節點，並且列表的所有子節點在平衡列表樹中必須具有相同的高度。請注意，括號對在平衡樹中被視為高度為 0 的葉子，但它可能在 AST 中有子節點。

在初始化期間從頭構建 AST 時，我們首先收集所有子節點，然後將它們轉換為這樣的平衡樹。這可以線上性時間內完成。

前面示例的可能 (2,3)-樹可能如下所示。請注意，我們現在只需要檢視 8 個節點（藍色）即可找到位置 24 處的括號對，並且列表是具有 2 個還是 3 個子節點有一些自由度

Balanced tree to describe lists in the AST

最壞情況複雜度分析

請隨意跳過有關演算法複雜度的部分。

目前，我們假設每個列表都類似於 (2,3)-樹，因此最多有 3 個子節點。

為了最大化查詢時間，我們來看一個具有 $\mathcal{O}(\mathrm{log} N)$ 許多巢狀括號對的文件

{
    {
        ... O(log N) many nested bracket pairs
            {
                {} [1]
            }
        ...
    }
}

尚未涉及列表，但我們已經需要遍歷 $\mathcal{O}(\mathrm{log} N)$ 許多節點才能找到 [1] 處的括號對。幸運的是，巢狀更深的文件是不典型的，因此我們在最壞情況分析中不考慮它們。

現在，在最壞的情況下，我們透過在每個巢狀的括號對中插入額外的 $N$ 直到文件大小達到 $\mathcal{O}(\frac{N}{\mathrm{log} N})$ 個括號對來填滿文件

{}{}{}{}{}{}{}{}... O(N / log N) many
{
    {}{}{}{}{}{}{}{}... O(N / log N) many
    {
        ... O(log N) many nested bracket pairs
            {
                {}{}{}{}{}{}{}{}... O(N / log N) many
                {} [1]
            }
        ...
    }
}

同一巢狀級別的每個括號列表都會產生一個高度為 $\mathcal{O}(\mathrm{log} \frac{N}{\mathrm{log} N}) = \mathcal{O}(\mathrm{log} N - \mathrm{log}\;\mathrm{log} N ) = \mathcal{O}(\mathrm{log} N)$ .

的樹。因此，要找到 [1] 處的節點，我們必須遍歷 $\mathcal{O}(\mathrm{log} N)$ 許多高度為 $\mathcal{O}(\mathrm{log} N)$ 的平衡樹。一旦我們找到節點並希望收集大小為 $R$ 的範圍內的所有括號，我們必須讀取最多 $\mathcal{O}(R)$ 個更多的相鄰葉節點，這些節點由最多 $\mathcal{O}(\mathrm{log}^2 N + R)$ 個內部節點連線。

因此，查詢括號的最壞情況時間複雜度為 $\mathcal{O}(\mathrm{log}^2 N + R)$ .

這也表明 AST 的最大高度為 $\mathcal{O}(\mathrm{log}^2 N)$ .

增量更新

高效能括號對顏色高亮最有趣的問題仍然懸而未決：給定當前的（平衡）AST 和替換某個範圍的文字編輯，我們如何有效地更新樹以反映文字編輯？

我們的想法是重用用於初始化的遞迴下降解析器，並新增快取策略，以便可以重用和跳過不受文字編輯影響的節點。

當遞迴下降解析器解析位置 $p$ 處的括號對列表，而下一個編輯位於位置 $e$ 時，它首先檢查先前的 AST 是否在文字更改前的位置 $e - p$ 處有一個長度至多為 $p$ 的節點。如果是這種情況，則不需要重新解析此節點，並且底層分詞器只需按節點的長度前進即可。消耗節點後，解析繼續進行。請注意，此節點既可以是單個括號對，也可以是整個列表。此外，如果有多個此類可重用節點，則應採用最長的節點。

下面的示例顯示了插入單個開括號時哪些節點可以重用（綠色）（省略了單個括號節點）

Reusable Nodes in AST

透過重新解析包含編輯的節點並重用所有未更改的節點來處理文字編輯後，更新後的 AST 如下所示。請注意，透過消耗 3 個節點 B、H 和 G，可以重用所有 11 個可重用節點，並且只需要重新建立 4 個節點（橙色）

Updated AST

如本例所示，平衡列表不僅使查詢速度快，而且有助於一次重用大塊節點。

演算法複雜度

請隨意跳過有關演算法複雜度的部分。

讓我們假設文字編輯替換了大小至多為 $E$ 的範圍，並插入了至多 $E$ 個新字元。我們現在也忽略沒有開括號對應的閉括號這種罕見情況。

我們只需要重新解析與編輯範圍相交的節點。因此，最多需要重新解析 $\mathcal{O}(\mathrm{log}^2 N + E)$ 個節點（與查詢括號的時間複雜度推理相同）——所有其他節點都可以重用。

顯然，如果一個節點不與編輯範圍相交，那麼它的任何子節點也不相交。因此，我們只需要考慮重用不與編輯範圍相交但其父節點相交的節點（這將隱式重用所有節點及其父節點都不與編輯範圍相交的節點）。此外，此類父節點不能被編輯範圍完全覆蓋，否則它們的所有子節點都將與編輯範圍相交。然而，AST 中的每一層最多隻有兩個節點部分與編輯範圍相交。由於 AST 最多有 $\mathcal{O}(\mathrm{log}^2 N)$ 層（受 AST 高度限制），並且每個節點最多有 3 個子節點，因此所有可重用節點最多可以透過消耗 $\mathcal{O}(2 \cdot 3 \cdot \mathrm{log}^2 N) = \mathcal{O}(\mathrm{log}^2 N)$ 個節點來覆蓋。

因此，要構建更新後的樹，我們最多需要重新解析 $\mathcal{O}(\mathrm{log}^2 N + E)$ 個節點，並且可以重用 $\mathcal{O}(\mathrm{log}^2 N)$ 個節點。

這也決定了更新操作的時間複雜度，但有一個注意事項。

我們如何重新平衡 AST？

不幸的是，最後一個示例中的樹不再平衡了。

當將重用的列表節點與新解析的節點組合時，我們必須做一些工作來維護 (2,3)-樹屬性。我們知道重用和新解析的節點都已經 (2,3)-樹，但它們可能具有不同的高度——所以我們不能只建立父節點，因為 (2,3)-樹節點的所有子節點都必須具有相同的高度。

我們如何有效地將所有這些具有混合高度的節點連線成一個單個的 (2,3)-樹？

這可以很容易地簡化為將較小的樹前置或附加到較大的樹的問題：如果兩棵樹具有相同的高度，則建立包含兩個子節點的列表就足夠了。否則，我們將高度為 $h_1$ 的較小樹插入到高度為 $h_2$ 的較大樹中，如果節點最終有超過 3 個子節點（類似於 (2,3)-樹的插入操作方式），則可能將其分解。

因為這具有執行時 $\mathcal{O}(h_2 - h_1)$ ，我們取 3 個相鄰節點（ $a$ , $b$ 和 $c$ ）要連線，然後先連線 $a$ 和 $b$ 或 $b$ 和 $c$ （可能增加樹的高度），具體取決於哪一對的高度差異較小。重複此操作直到所有節點都連線起來。作為額外的最佳化，我們尋找具有相同高度的節點序列，並在線性時間內為它們建立父列表。

為了平衡上一個示例中的列表 α 和 γ，我們對其子節點執行連線操作（紅色列表違反 (2,3)-樹屬性，橙色節點高度意外，綠色節點在重新平衡時重新建立）

AST after balancing lists

因為列表 B 在不平衡樹中的高度為 2，而括號對 β 的高度為 0，所以我們需要將 β 附加到 B，並完成列表 α。剩餘的 (2,3)-樹是 B，因此它成為新的根並替換列表 α。繼續處理 γ，其子節點 δ 和 H 的高度為 0，而 G 的高度為 1。

我們首先連線 δ 和 H，並建立高度為 1 的新父節點 Y（因為 δ 和 H 具有相同的高度）。然後我們連線 Y 和 G，並建立新的父列表 X（出於同樣的原因）。然後 X 成為父括號對的新子節點，替換不平衡的列表 γ。

在這個例子中，平衡操作有效地將最頂層列表的高度從 3 減少到 2。然而，AST 的總高度從 4 增加到 5，這對最壞情況查詢時間產生負面影響。這是由括號對 β 引起的，它在平衡列表樹中充當葉子，但實際上包含另一個高度為 2 的列表。

在平衡父列表時考慮 β 的內部 AST 高度可以改善最壞情況，但這將脫離 (2,3)-樹的理論。

演算法複雜度

請隨意跳過有關演算法複雜度的部分。

我們必須連線至多 $\mathcal{O}(\mathrm{log}^2 N)$ 個具有最大列表高度為 $\mathcal{O}(\mathrm{log} N)$ 的節點（那些我們重用的節點）和額外的 $\mathcal{O}(\mathrm{log}^2 N + E)$ 個列表高度為 0 的節點（那些我們重新解析的節點）。

因為連線兩個不同高度的節點的時間複雜度為 $\mathcal{O}(\mathrm{log} N)$ 並且列表中的所有重新解析節點都是相鄰的並且列表高度為 0，所以整個更新操作的時間複雜度至多為 $\mathcal{O}(\mathrm{log}^3 N + E)$ ，前提是查詢可重用節點足夠快。

我們如何有效地找到可重用節點？

我們有兩個資料結構用於此任務：*編輯前位置對映器*和*節點讀取器*。

位置對映器將新文件中的位置（應用編輯後）對映到舊文件中的位置（應用編輯前），如果可能的話。它還告訴我們當前位置與下一個編輯之間的長度（如果我們處於編輯中，則為 0）。這可以在 $\mathcal{O}(1)$ .

中完成。當處理文字編輯和解析節點時，該元件為我們提供了可以潛在重用的節點位置及其最大允許長度——顯然，我們想要重用的節點必須短於到下一個編輯的距離。

節點讀取器可以快速找到 AST 中在給定位置滿足給定謂詞的最長節點。為了找到我們可以重用的節點，我們使用位置對映器來查詢其舊位置及其最大允許長度，然後使用節點讀取器來查詢該節點。如果我們找到了這樣的節點，我們就知道它沒有改變，可以重用它並跳過它的長度。

因為節點讀取器是以單調遞增的位置查詢的，所以它不必每次都從頭開始搜尋，而是可以從上一個重用節點的末尾開始搜尋。實現這一點的關鍵是無遞迴的樹遍歷演算法，它可以深入節點，也可以跳過節點或返回父節點。當找到一個可重用節點時，遍歷停止並繼續下一個對節點讀取器的請求。

單次查詢節點讀取器的複雜度高達 $\mathcal{O}(\mathrm{log}^2 N)$ ，但我們非常確定單個更新操作發出的所有請求的均攤複雜度也是 $\mathcal{O}(\mathrm{log}^2 N)$ 。畢竟，節點讀取器只查詢不受文字編輯影響的位置，並且始終採用從上一個可重用節點到下一個可重用節點的最短路徑。因此，我們認為節點讀取器足夠高效，不會影響更新演算法的執行時複雜度。

令牌更新

當在不包含文字 */ 的長 C 風格文件開頭插入 /* 時，整個文件會變成一個註釋，所有令牌都會更改。

因為令牌是在渲染器程序中同步計算的，所以不能一次性重新分詞而不會凍結 UI。

相反，令牌是隨時間分批更新的，這樣 JavaScript 事件迴圈就不會被阻塞太久。雖然這種方法不會減少總阻塞時間，但它提高了更新過程中 UI 的響應能力。最初對文件進行分詞時也使用相同的機制。

幸運的是，由於括號對 AST 的增量更新機制，我們可以立即應用此類分批令牌更新，方法是將更新視為單個文字編輯，該編輯將重新分詞的範圍替換為自身。一旦所有令牌更新都傳入，括號對 AST 就保證處於與從頭開始建立時相同的狀態——即使在重新分詞進行時使用者編輯了文件。

這樣，不僅分詞即使文件中的所有令牌都更改也具有高效能，而且括號對顏色高亮也具有高效能。

然而，當文件在註釋中包含大量不平衡的括號時，文件末尾的括號顏色可能會閃爍，因為括號對解析器會發現這些括號應該被忽略。

為了避免開啟文件並導航到其末尾時括號對顏色閃爍，我們在初始分詞過程完成之前維護兩個括號對 AST。第一個 AST 是在沒有令牌資訊的情況下構建的，並且不接收令牌更新。第二個 AST 最初是第一個 AST 的克隆，但接收令牌更新，並隨著分詞的進行和令牌更新的應用而越來越偏離。最初，第一個 AST 用於查詢括號，但一旦文件完全分詞，第二個 AST 就會接管。

因為深度克隆幾乎與重新解析文件一樣昂貴，所以我們實現了寫入時複製，從而實現了 $\mathcal{O}(1)$ .

中進行克隆。

長度編碼

編輯器檢視用行號和列號描述視口。顏色裝飾也期望以基於行/列的範圍表示。 $\mathcal{O}(\mathrm{log} N)$ 為了避免偏移量和基於行/列的位置之間的轉換（這可以在

中完成），我們也對 AST 使用基於行/列的長度。

請注意，此方法與直接按行索引的資料結構（例如使用字串陣列描述文件的行內容）有顯著不同。特別是，這種方法可以在行之間和行內進行單個二分查詢。

新增兩個這樣的長度很容易，但需要區分情況：雖然行數直接相加，但只有當第二個長度跨越零行時，第一個長度的列數才包含在內。

令人驚訝的是，大多數程式碼不需要知道長度是如何表示的。只有位置對映器變得明顯更復雜，因為必須注意單行可以包含多個文字編輯。 $作為實現細節，我們將這些長度編碼為一個數字，以減少記憶體壓力。JavaScript 支援最大為$ $2^{53} - 1$ $2^{53} - 1$ $2^{31}$ 的整數，因此我們可以為行數和列數各使用多達 26 位。不幸的是，v8 將大於的值儲存在堆中，因此這種編碼技巧並未像我們想象的那樣有效。

進一步的困難：未閉合的括號對

到目前為止，我們假設所有括號對都是平衡的。然而，我們也希望支援未閉合和未開啟的括號對。遞迴下降解析器的優點在於我們可以使用錨點集來改進錯誤恢復。

考慮以下示例

( [1]
} [2]
) [3]

顯然 [2] 處的 } 不關閉任何括號對，表示一個未開啟的括號。[1] 和 [3] 處的括號很好地匹配。然而，當在文件開頭插入 { 時，情況發生了變化

{ [0]
( [1]
} [2]
) [3]

現在，[0] 和 [2] 應該匹配，而 [1] 是一個未閉合的括號，[3] 是一個未開啟的括號。

特別是，在下面的示例中，[1] 應該是一個在 [2] 之前終止的未閉合括號

{
    ( [1]
} [2]
{}

否則，開啟一個括號可能會改變不相關後續括號對的巢狀級別。

為了支援這種錯誤恢復，可以使用錨點集來跟蹤呼叫者可以繼續使用的預期令牌集。在前面示例中位置 [1] 處的錨點集將是 $\{$ } $\}$ 。因此，當解析 [1] 處的括號對發現 [2] 處的意外括號 } 時，它不會消耗它並返回一個未閉合的括號對。

在第一個示例中，[2] 處的錨點集是 $\{$ ) $\}$ ，但意外字元是 }。因為它不屬於錨點集，所以它被報告為未開啟的括號。

在重用節點時需要考慮這一點：當在 ( } ) 前面加上 { 時，它不能重用。我們使用位集來編碼錨點集，併為每個節點計算包含未開啟括號的集合。如果它們相交，我們就不能重用該節點。幸運的是，只有少數幾種括號型別，所以這對效能影響不大。

未來展望

高效的括號對顏色高亮是一個有趣的挑戰。藉助新的資料結構，我們還可以更有效地解決其他與括號對相關的問題，例如常規括號匹配或顯示彩色行作用域。

儘管 JavaScript 可能不是編寫高效能程式碼的最佳語言，但透過降低漸近演算法複雜度可以獲得很大的速度提升，尤其是在處理大型輸入時。

編碼愉快！

Henning Dieterichs，VS Code 團隊成員 @hediet_dev